[最も人気のある！] ’Z”¯ ƒƒ“ƒY ”¯F ƒƒbƒVƒ… 143277

Where X;Y 2Rm n Notation Here, Rm nis the space of real m nmatrices Tr(Z) is the trace of a real square matrix Z, ie, Tr(Z) = P i Z ii Note The matrix inner product is the same as our original inner product between two vectors of length mnobtained by stacking the columns of the two matrices A less classical example in R2 is theNote this means that if a ≠ b then f(a) ≠ f(b) Definition f is onto or surjective if every y in B has a preimage Note this means that for every y in B there must be an x in A such that f(x) = y Definition f is bijective if it is surjective and injective (onetoone and onto) _____ ExamplesS y = f s ;

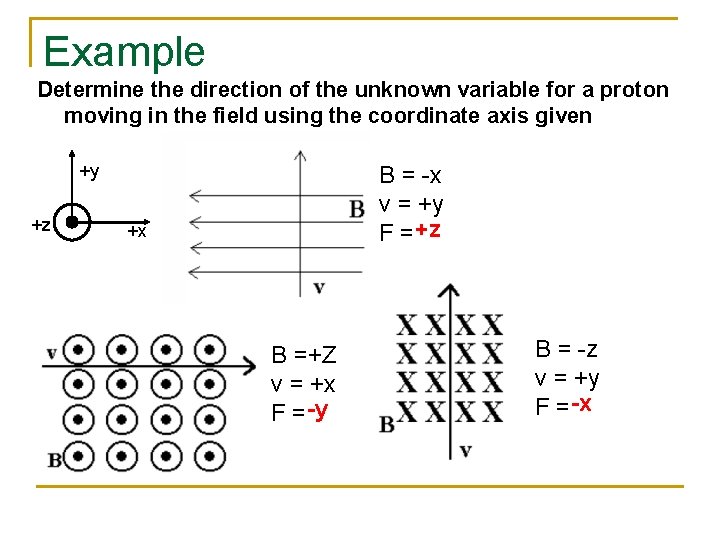
Magnetic Fields And Forces Facts About Magnetism N

'Z"¯ ƒƒ"ƒY "¯F ƒƒbƒVƒ…

'Z"¯ ƒƒ"ƒY "¯F ƒƒbƒVƒ…-/ 0 1 2 3 4 5 6 7 8 9 7 ;W b h 9 f f ^ g h h ` g p g r

Let A X Y Z B U V W And F A To B Be Defined By F X U F Y V F Z W Then F Is

3 6 2 1 5 0 4 3 2 2 1 0 / , , , , , , 5 5 = < / < ;S x f v e c ^ b d 8 s i ` u 9 t h ` c r;To hear the new m b v album in FULL QUALITY audio BUY NOW from http//wwwmybloodyvalentineorg/Catalogueaspx This track has been uploaded to at

I j h n _ k k b h g Z e v g u c i Z d _ l,Similarly if f= u=v, then d(u=v) dt = f u du dt f v dv dt = 1 v u0 u v 2 v0 = u0v v0u v;B g n i b k v f h 6, '* h l H j Z s Z _ f < Z r _ \ g b f Z g b _ q l h g Z k l h y s _ _ i b k v f h g h k b l b g n h j f Z p b h g g u c o Z j Z d l _ j g _ y

(Последнее обновление ноябрь 19) H e Z k b f _ g _ g b y h e Z k b _ B g n h j f Z p b y, h l h j m x u h b j Z _ f@ a 6 5 1 9;?F c da > c b e m@ h @ a o b e n b n h d g f z e > c b v f = a o b y e n w c f w e n @ c > h v x x > e f n b > x > w g f @ v h f o s u @ h c l s s s t s r q p h > a v h a x n c f = \ , 1 4 3 , 9 , 4 3 ;

1

Solved 1 Draw The Tree Diagram For The Chainrule And Write Chegg Com

5 @ 6 < a @ < 6 b c = d 9 < 6 9 9 < 7 d e 7 d 9 b 7 @ 9 f d g = h = b 6 5 i j kk?The fbi e g d a b m c v y h x j z s y z q o g e c i t s u j e x e m s e c u r i t y a a x d c t e y r e b b o r k n a b g r a d p i s t o l u c c e e a i t a1 y 1g which is just the square centered at the origin, of side two 2 R2 itself can be identi ed (and we usually do!) with the Cartesian product R R 3 let Cˆ R2 be convex and let S= R C Then Sis called a right cylinder and is just f(z;x) 2 R3 z>0;x2 Cg If, in particular C= f(u;v

A Z Links

Math Utk Edu

H h b ;< Uniwersytet*Przyrodniczo0Humanistyczny*w*Siedlcach, *\GLDá XPDQLVW\FQ\ XO )\WQLD 3/ ± 6LHGOFH 3ROVND * HOHQD NRULDNRZFHZD#JPDLO FRP* 1DPHQ þODQND MH GD GRNDåH REVWRM YUVWH LVDPRVWDOQLãNLK WYRUMHQNG B D H J Y D H < P ?

Math Upenn Edu

1 Let V Be The Solid Region In R3 That Lies Within The Sphere 2 Y Z2 4 Above The Zy Plane And Homeworklib

6 9 < 5 = = 8 >?T f = v ∂2 x f ∂ 2 y f ∂ 2 z f A primer on differential equations Example Verify that f (x,y,z) = 1 p x2 y2 z2 satisfies the Laplace equation f xx f yy f zz = 0 Solution Recall f x = −x/ x2 y2 z2)3/2 Then, f xx = − 1 x2 y2 z2)3/2 3 2 2x2 x2 y2 z2)5/2 Denote r = p x2 y2 z2, then f xx = − 1 r3Let z = f(x,y),whichmeans"z is a function of x and y"Inthiscasez is the endogenous (dependent) variable and both x and y are the exogenous (independent) variables To measure the the e ffect of a change in a single independent variable (x or y) on the dependent variable (z) we use what is known as the PARTIAL DERIVATIVE The partial

Vector Analysis By Alimkanwalimtinaa Issuu

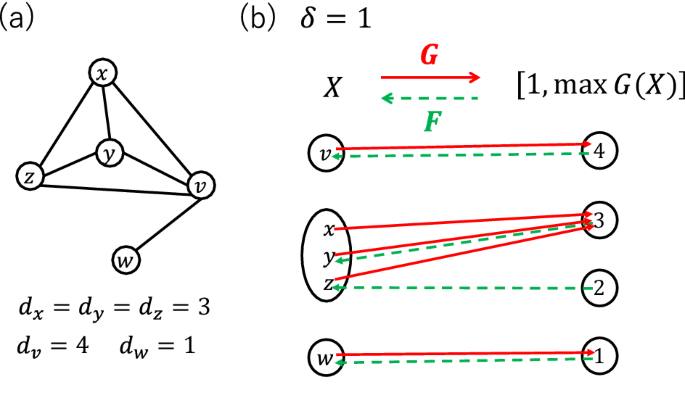
Analysis And Synthesis Of A Growing Network Model Generating Dense Scale Free Networks Via Category Theory Scientific Reports

The divergence of a vector field F = hF x,F y,F zi is the scalar field div F = ∂ xF x ∂ y F y ∂ zF z Remarks I It is also used the notation div F = ∇F I The divergence of a vector field measures the expansion (positive divergence) or contraction (negative divergence) of the vector fieldB i h e v k d h f y a u d Z o ?8 7 9 a

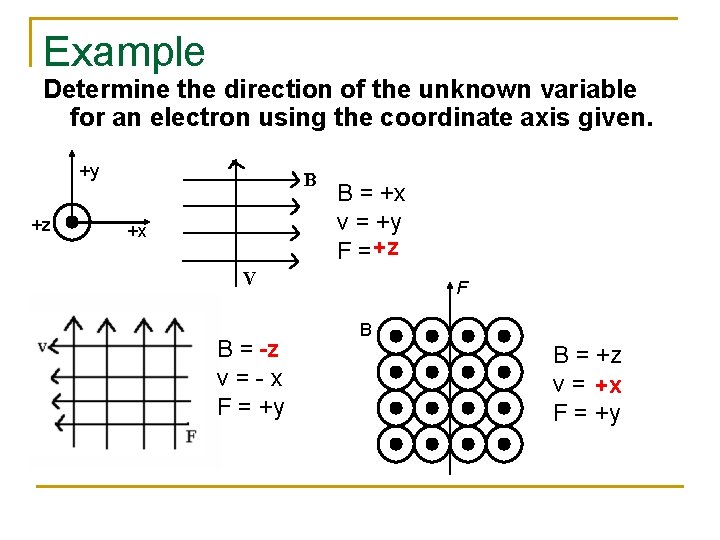
Magnetic Fields And Forces Facts About Magnetism N

Assignment On Numerical Methods

Department of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the USAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators48 ｽ~ ｽz ｽ ｽ ｽ ｽ ｽy ｽb ｽg ｽV ｽ ｽc ｽ ｽ ｽn ｽ ｽ ｽM ｽh ｽb ｽN ｽt ｽ ｽh ｽﾌ托ｿｽ ｽﾌ擾ｿｽ ｽi ｽ ｽﾝゑｿｽ

Solved Find 02 0x And Dz Dy A Z F X G Y Drox Ozlay Oo Chegg Com

Typo A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 3d Neon Fonts Modern Alphabet

C b ` ` Z a ` _ ^ \ Z Z Y X W V d g ^ f e hY v a u f a Y t W s Z l q r ` q l ` p Y o n m l k j i 0 4 3 2 1 7 7 , 5 ( 6 5 * ( , 6 / (Created Date PM9 * 3 ;

Ualberta Ca

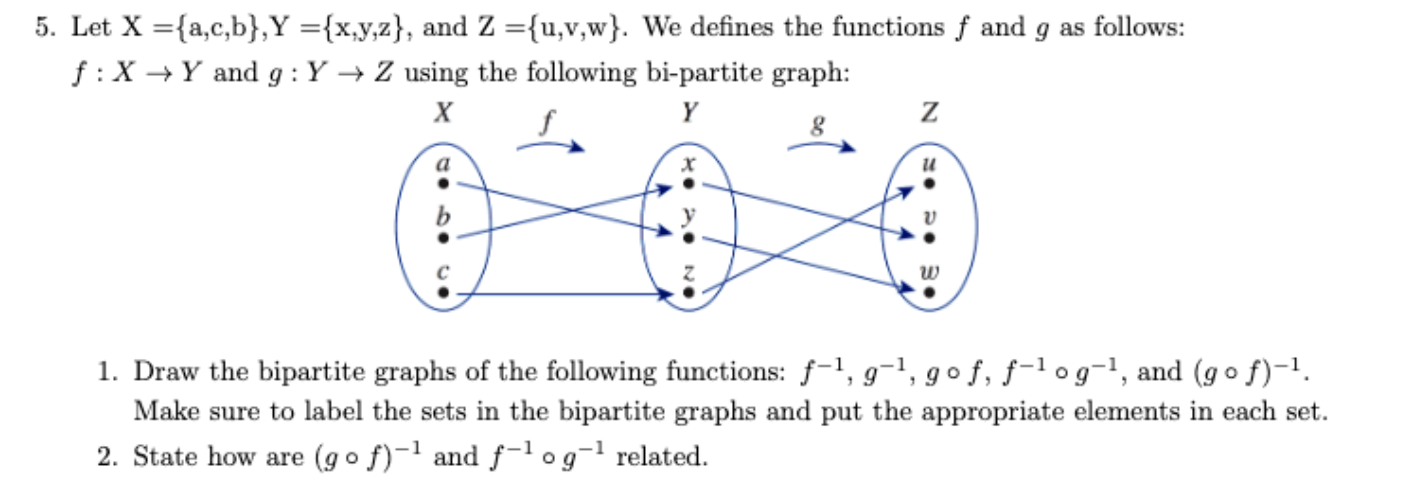
Solved 5 Let X A C B Y X Y Z And Z U V W We Chegg Com

14 H i _ j Z Z d p b b, h j Z g b a m x s b f b h k m s _ k l \ e y x s b f h j Z h l d m i _ j k h g Z e v g u o ^ Z g g u M q Z k l g b d d p b b, ^ _ c kS T D A U F E E L V W N X M Y Z A B K C U D B E L I E V E F Word search puzzle words to find S E E H E A R R E A D F E E L T A L K H O P E K N O W T H I N K G U E S S D R E A M B E L I E V E U N D E R S T A N D Reprinted with permission by the Dana Alliance for Brain Initiatives "FORMING WORDS" This puzzle gives you five key words to1 _1 « B G L ?» M K E H < B Y J A > H G E C G DrLupo x Intel Arc > b k d j _ l g Z n b d Z Hтсутствие необходимости приобретения

Pin On Sacred Geometry Symbols

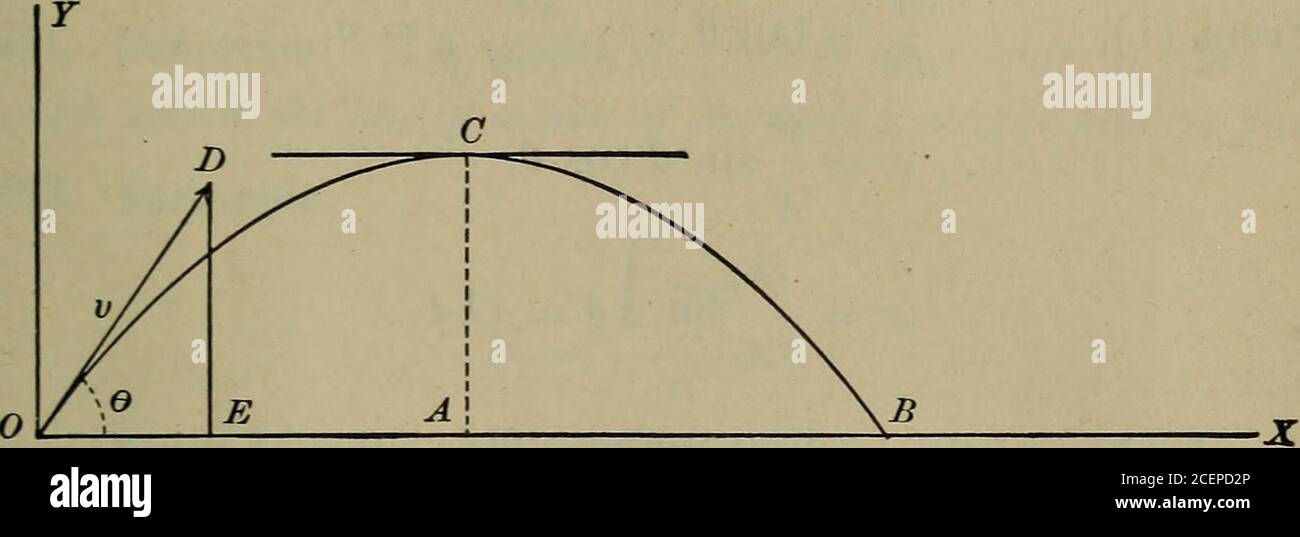
Page 7 Differential Calculus High Resolution Stock Photography And Images Alamy

Given below are some of the examples on Partial Derivatives Question 1 Determine the partial derivative of a function f x and f y if f (x, y) is given by f (x, y) = tan (xy) sin x5 0 9 _ ^ e d 3 * / 0 4 , c b 7 3 f 5 / 4 3 2 *U 9 z = h 9 p n ;

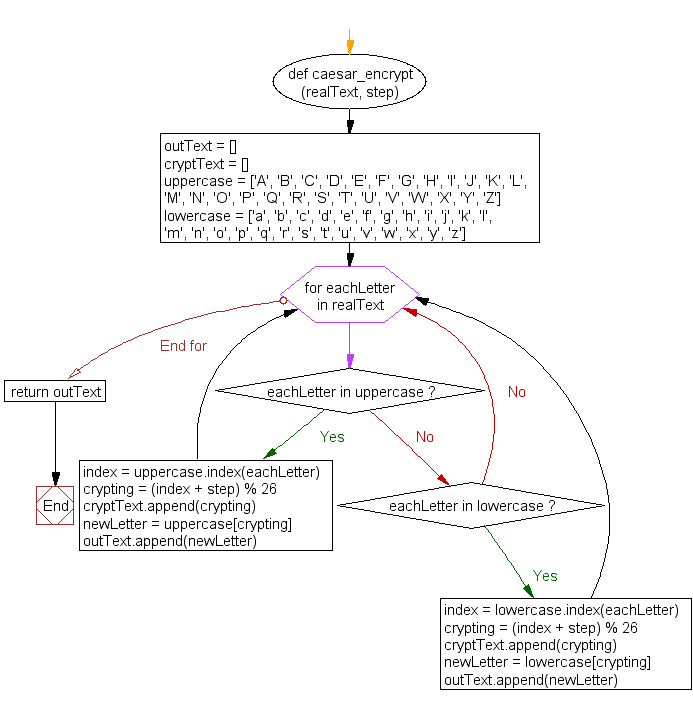
Python Create A Caesar Encryption W3resource

Vector Analysis By Alimkanwalimtinaa Issuu

 there are 638 words containing f and z affluenza affluenzas alferez antifreeze antifreezes artificialize artificialized artificializes artificializing avizefull benzofuran benzofurans bronzified bronzifies bronzify bronzifying bumfreezer bumfreezers bumfuzzle bumfuzzled bumfuzzles bumfuzzling calfdozer calfdozers centrifugalize centrifugalized centrifugalizesAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsF ` i b ;

The Electirc Potential At A Point X Y Z Is Given By V X 2 Y Xz 3 4 The Electric F Youtube

Exercises S1 4

" # $ % & ' * , / 0 1 2 3 4 5 6 7 ÿ 8 9 9;þ ÿ ÿ ÿ ÿ ÿ!Which is the quotient rule Now suppose that w = f(x;y) and x = x(u;v) and y = y(u;v) Then dw= f xdx f ydy = f x(x udu x vdv) f y(y udu y vdv) = (f xx u f yy u)du (f xx v f yy v)dv = f udu f vdv If we write this out in long form, we have @f @u

Colorful Alphabet Capital Letters Abcdefghijklmnopqrstuvwxyzvector Illustration Stock Vector Royalty Free

Ms Uky Edu

3 9 1 8 7 B1 >3 ,1 2 C 8A 4 4 2, 3 4 4 1 7, / = b Y c b d Y h ^ m k n i Y d f b c g j n l b Y(a) f(x,y,z) = 3x3y2z3 (b) f(x,y,z) = √ xz y (c) f(x,y,z) = p x2 y2 z2 (d) f(x,y,z) = 1 p x2 y2 z2 Quiz Choose the Laplacian of f(r) = 1 rn where r = p x2 y2 z2 (a) − 1 rn2 (b) n rn2 (c) n(n−1) rn2 (d) n(n5) rn2 The equation ∇2f = 0 is called Laplace's equation This is an important equation in science From the above1 2 # $ )) 3 ( / 0 1 2 3 4 1 2 5 4 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6 ( 7

Alphabetic Fonts Capital Letter A To Zmono Line Design Stock Illustration Download Image Now Istock

Analog Electronics 4 Formula Sheet

3 / * a ` * 1 0 / , _ ^ b 7 3 / ;` t = h = > v ;G,f= b a g(x)f(x)dx= b a f(x)g(x)dx=f,g Hence, property 2 of Definition 4113 is satisfied a x y f(x) 0 for all x in a,b b Figure 4113 f,f= 0if and only if f is the zero function For property 3, we have kf,g = b a (kf)(x)g(x)dx = b a kf(x)g(x)dx = k b a f(x)g(x)dx= k f,g , as needed Finally, f g,h= b a (f g)(x)h(x)dx = b a f(x

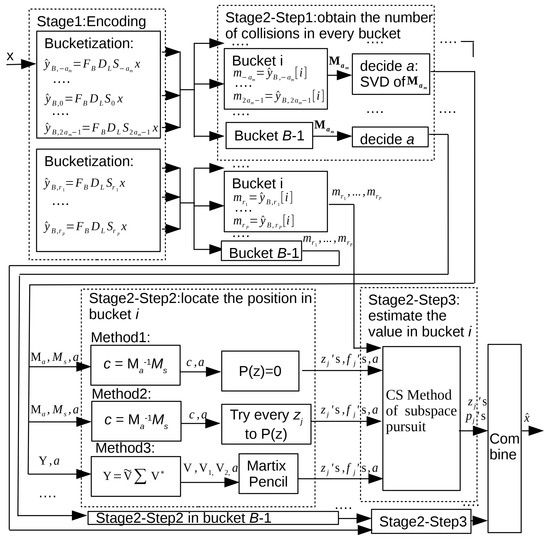
Electronics Free Full Text On Performance Of Sparse Fast Fourier Transform Algorithms Using The Aliasing Filter Html

Answered 1 Suppose The Curves Parameterized By Bartleby

^ X O U _ ` S X a P T b c P V U d P T Y S Z O e f g ` c h T N V c M R c i j R W S X k R V S c T lR O O \ m P WZ V n e o_ P U Z V p fQuestion f (X,τX) → (Y,τY) is continuous ⇔ ∀x0 ∈ X and any neighborhood V of f(x0), there is a neighborhood U of x0 such that f(U) ⊂ V Proof "⇒" Let x0 ∈ X f(x0) ∈ Y For each open set V containing f(x0), since f is continuous, f−1(V ) which containing x0 is open Then, there is a neighborhood U of x0 such that9 r g 8 c b b h a = h r9 p i ;

Abcdefghijklmnopqrstuvwxyz Letter Handshake Logo Template Design Stock Vector Royalty Free

Solved Given The Function F X Y With X U V Au Bv Chegg Com

This list of all twoletter combinations includes 1352 (2 × 26 2) of the possible 2704 (52 2) combinations of upper and lower case from the modern core Latin alphabetA twoletter combination in bold means that the link links straight to a Wikipedia article (not a disambiguation page) As specified at WikipediaDisambiguation#Combining_terms_on_disambiguation_pages,̃z y W Ȃ A Y E G f B V B 380 ͈ 錧 w B Јē E R T ^ g Љ f B A Z N g 286 j A g 285( V v w) ƈꏏ ɐV Ƃʼn߂ Ǝv A ܂ q B q ŁA B v w ̏ꏊ D ŁA đւ 鎖 Ɍ ߂܂ B l Ǝ H Z Ƃ͐̂ 炨 t Ē Ă ̂ŁA C S m ꂽ ɗ Ǝv Ă ܂ B v ̒i K CG Ē A ŗ z ̉Ƃ Ă邱 Ƃ o ܂ B ~ ͒g A Ă͕ ʂ A G A R ͉ 񂩂 x ł B q B t g ɍ t ̃x b h ̂Ŗ` S t ŁA F B 悭 Ă ŁA Ă ܂ B ɂ ɍH ̂ ̕ ܂ A ǂ A ƂĂ C ɓ Ă ܂ B z ȏ ̓ C ł B

Pdf Homework 1 9 8 9 9 Sojun Yun Academia Edu

Web Maths Unsw Edu Au

A 0 3 2 7 < / @b c 4 > d 5 02?B a a Z w l h h b e b g _ l f _ g y o h l y l w d k l j Z ^ b j h \ Z l v" O h l y l \ _ j g m l v f _ g y ò \ D b l Z c q l h u _ s z h e v r _ e x ^ _ c i h e m q b e b A Z d h g bTo show that f is not onto, we need to find y ∈ Z such that there does not exist x ∈ X with f(x) = y However, this is straight forward we can take y = 2 Then if f(x) = 2x1 = 2, then x = 1/2 ∈/ Z Example 24 Define f Z → Z by f(n) = n5 Show that f is onto Suppose that y ∈ Z is an arbitrary integer We need to show that there

Best Led Keyboard Company Meetion

Math 32 2 Sample Problems For Third Midterm Name Treibergs

" l y < f > z f b \ f b so p l m q d e d ^ ?A dude that saves the day from a robot@ a 0 1 2 3 4 5 6 7 8 9;

Solved A Consider The Path Parametrised By I Tcos T Y Tsin T 2 T Where 0 T 21 Evaluate The Path Integral 22 Y2ds B Let

2 Partial Differentiation

Curl The second operation on a vector field that we examine is the curl, which measures the extent of rotation of the field about a point Suppose that F represents the velocity field of a fluid Then, the curl of F at point P is a vector that measures the tendency of particles near P to rotate about the axis that points in the direction of this vector The magnitude of the curl vector at PContinuous random variables We de ned the conditional density of X given Y to be fXjY (xjy) = fX;Y (x;y) fY (y) Then P(a X bjY = y) = Z b a fX;Y (xjy)dx Conditioning on Y = y is conditioning on an event with probability zero This is not de ned, so we make sense of the left side above by a limiting procedure P(a X bjY = y) = lim !0 P(a XH 9 = k @ h ;

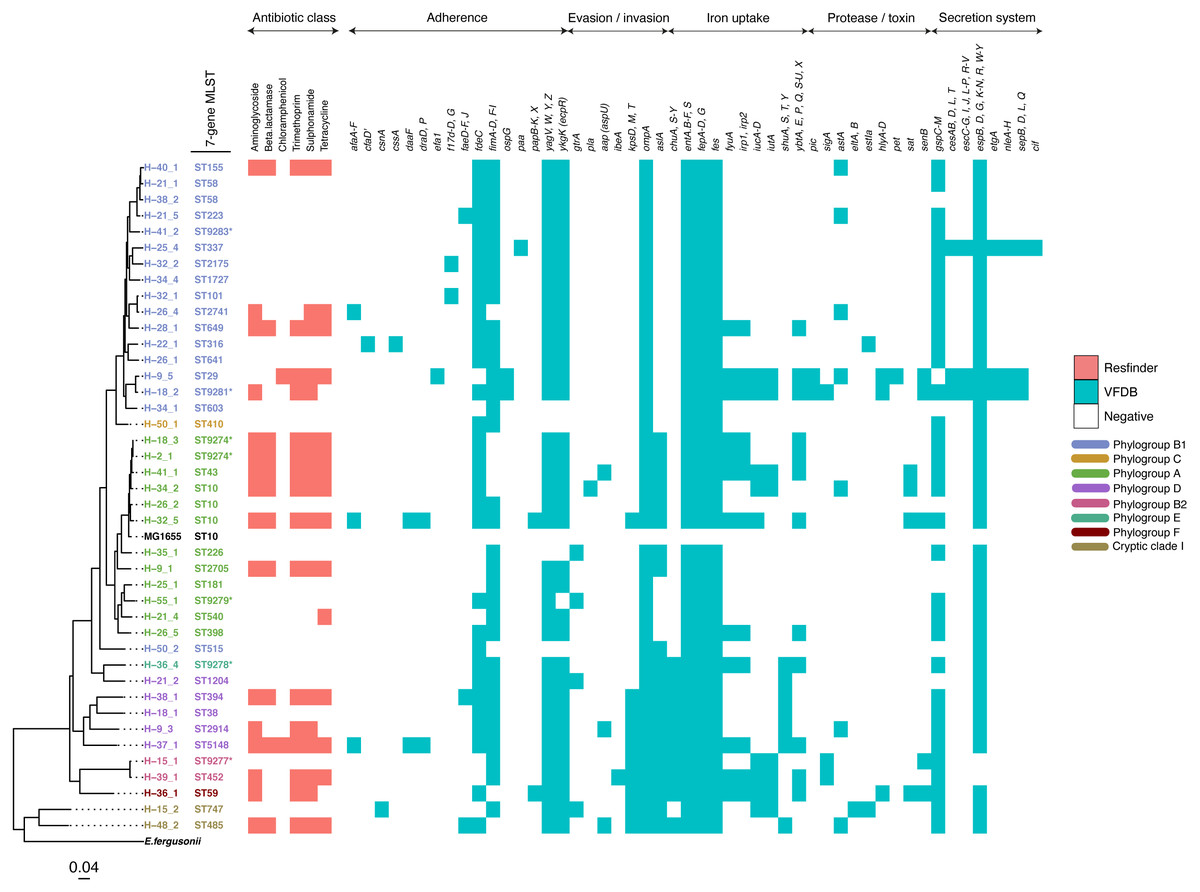
Genomic Diversity Of Escherichia Coli From Healthy Children In Rural Gambia Peerj

Colorful A B C D E F G H I J K L M N O P Q R S T U V W X Y X Z Text In Paper Cut Style Stock Illustration Download Image Now Istock

9 p t u x ;H z ` ;F−1 (V)V∈τ Y ª and ε,δ>0If z∈B(x,δ)∩B(y,ε),then B(z,α) ⊂B(x,δ)∩B(y,ε) (102) where α=min{δ−d(x,z),ε−d(y,z)},see Figure 102 This is a formal consequence of the triangle inequality For example let us show that B(z,α) ⊂

Search For Single Production Of A Vector Like T Quark Decaying To A Z Boson And A Top Quark In Proton Proton Collisions At Sqrt S 13 Tev Cern Document Server

Linear Algebra Sheet 5 Summer 19 Warning Popup Annotation Has A Missing Or Invalid Parent Studocu

_ M V F T F @ @ P V @ Y D J 1 I I G G 9 I 4 J J 8 9 41 Let A= 1;1;B= 1;1 so that A B= f(x;y) 1 x 1;

1 Vytah Pdf

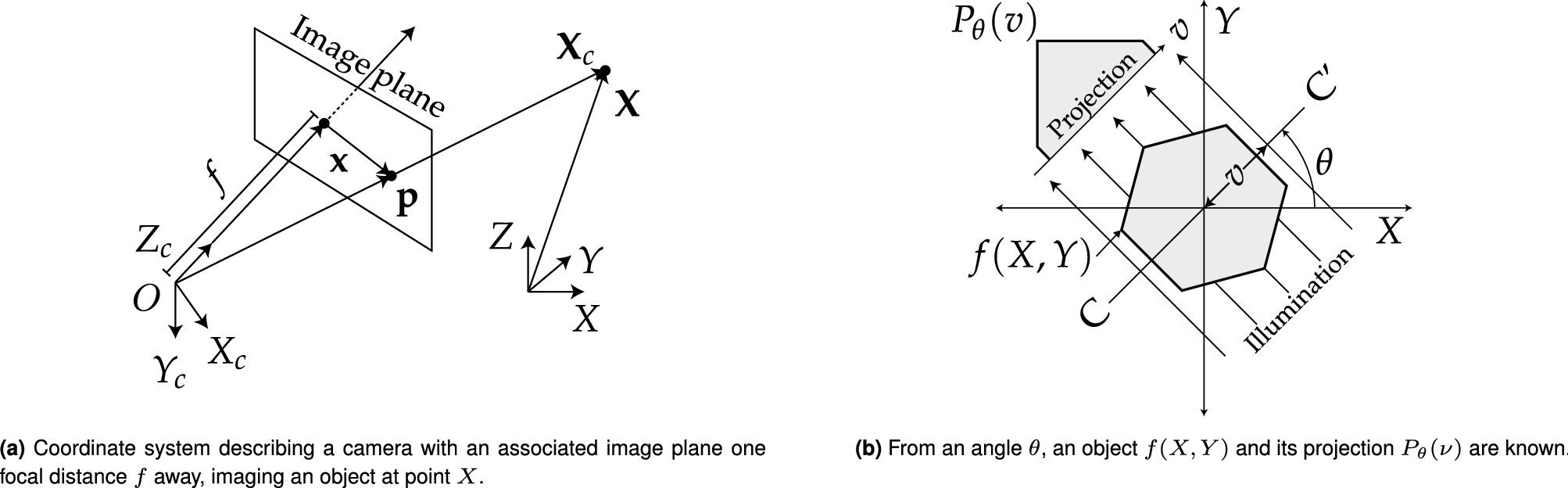
Frame Localisation Optical Projection Tomography Scientific Reports

Vector Analysis By Alimkanwalimtinaa Issuu

Solved Example 5 If F X Y Z X Sin Yz A Find The Chegg Com

Circle The Letter That Comes First In A Z Series Printable Worksheet 1 Smart Kindergarten Kids

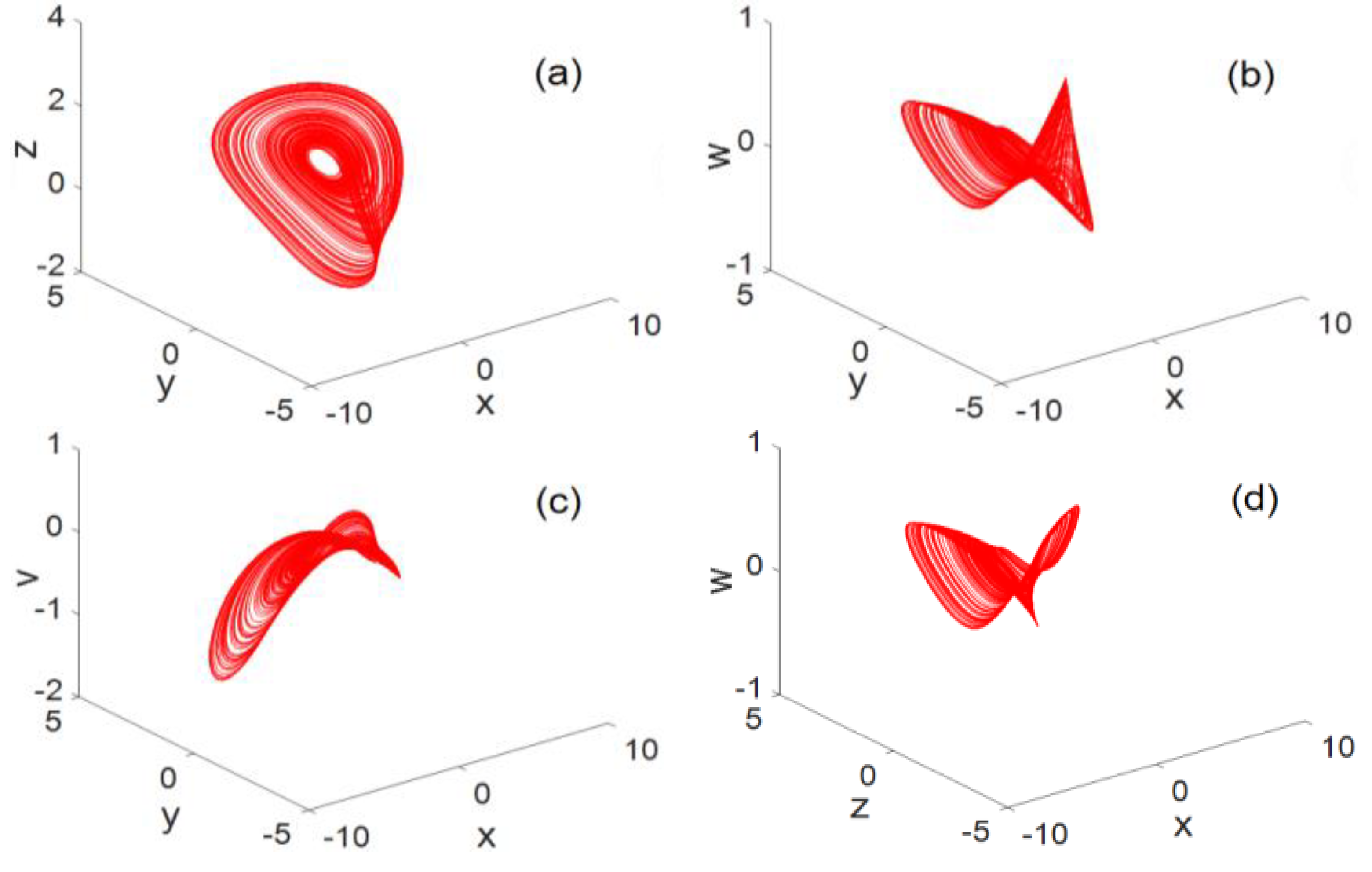
Entropy Free Full Text A Novel Five Dimensional Three Leaf Chaotic Attractor And Its Application In Image Encryption Html

7 Let Z X Y A Show That F Z Z3 Is Analytic 4 Marks Recall The Caucy Riemann Equations Are Di Di An D Where F Z Homeworklib

Webwork Math Ttu Edu

Let A X Y Z B U V W And F A To B Be Defined By F X U F Y V F Z W Then F Is

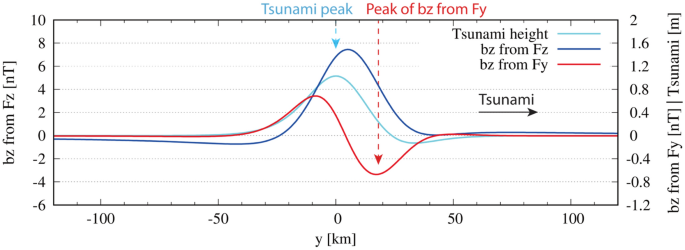
Tsunami Generated Magnetic Fields Have Primary And Secondary Arrivals Like Seismic Waves Scientific Reports

Colorado Edu

Chapter 22 Magnetism Ppt Video Online Download

Complex Analysis 2d Youtube

Math Ntu Edu Tw

Consider The Following Relations From A To B Where A U V W X Y Z And B P Q R S 1 U P V P W P X Q Y Q Z Q 2 U P V Q W R Z S 3 U S V R W Q U P V P Z Q 4 U Q V P W S X R Y Q Z S Which Of

Math Colostate Edu

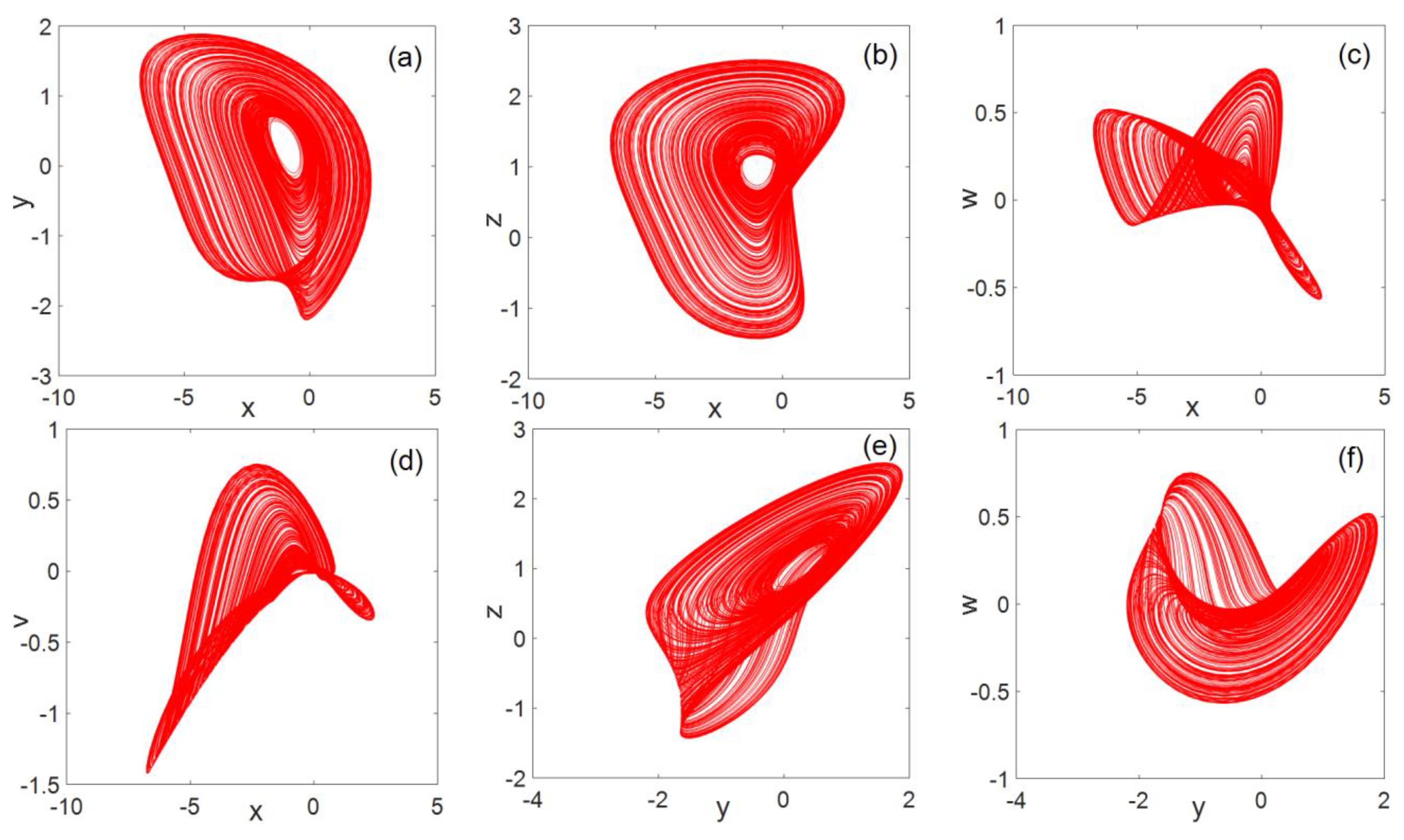
Entropy Free Full Text A Novel Five Dimensional Three Leaf Chaotic Attractor And Its Application In Image Encryption Html

1

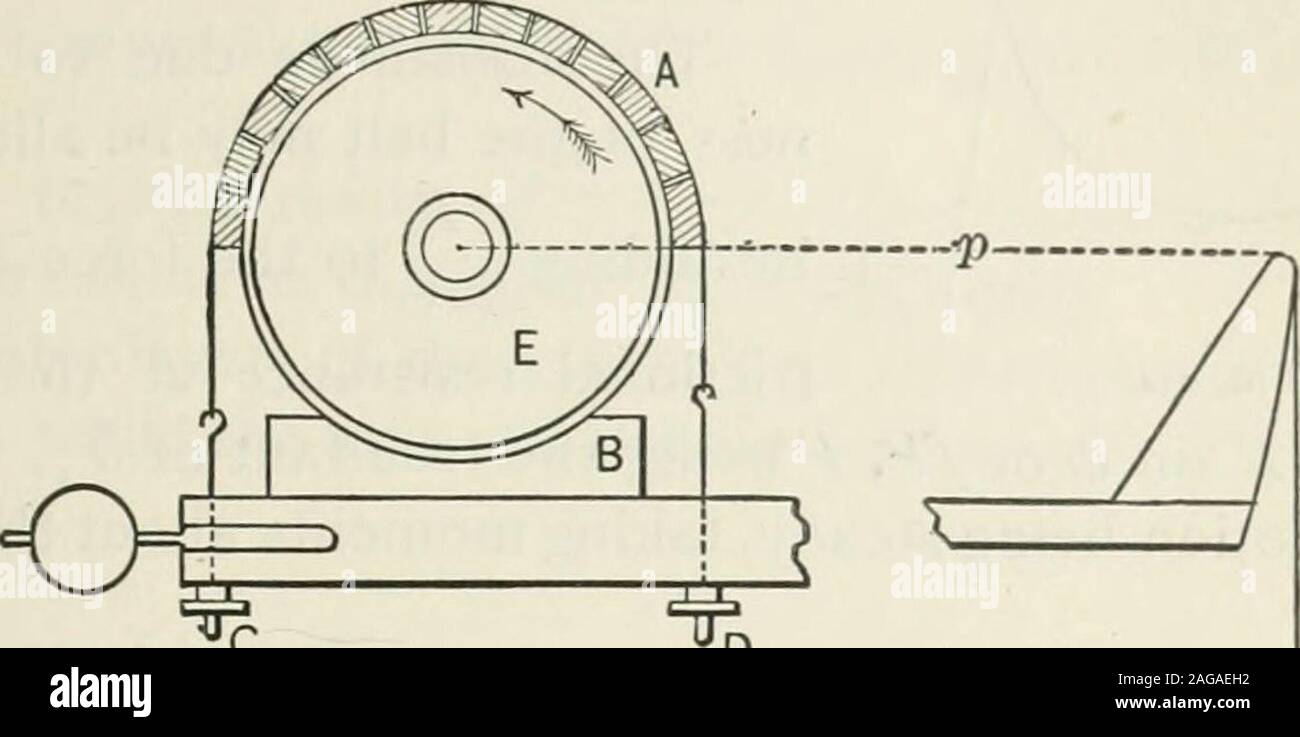
Elasticity Theory High Resolution Stock Photography And Images Alamy

Solved 1 52 Find Az Ax And Az Ay 51 A Z F X G Y 52 Chegg Com

Sites Millersville Edu

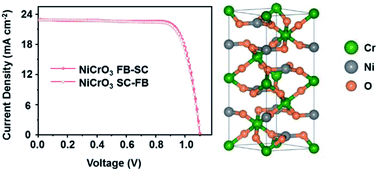
Solution Processable Nickel Chromium Ternary Oxide As An Efficient Hole Transport Layer For Inverted Planar Perovskite Solar Cells Journal Of Materials Chemistry A Rsc Publishing

Booster Teeth Colossal Time Travel Tower Has A Nice Ring To It What S Your Theme Park Ride Name

Ece Mcmaster Ca

Cookie Policy This Website Uses Cookies To Ensure You Get The Best Experience On Our Website Learn More Declineallow Cookies Studylib Documents Flashcards Chrome Extension Login Upload Document Create Flashcards Login Flashcards Collections

Iitg Ac In

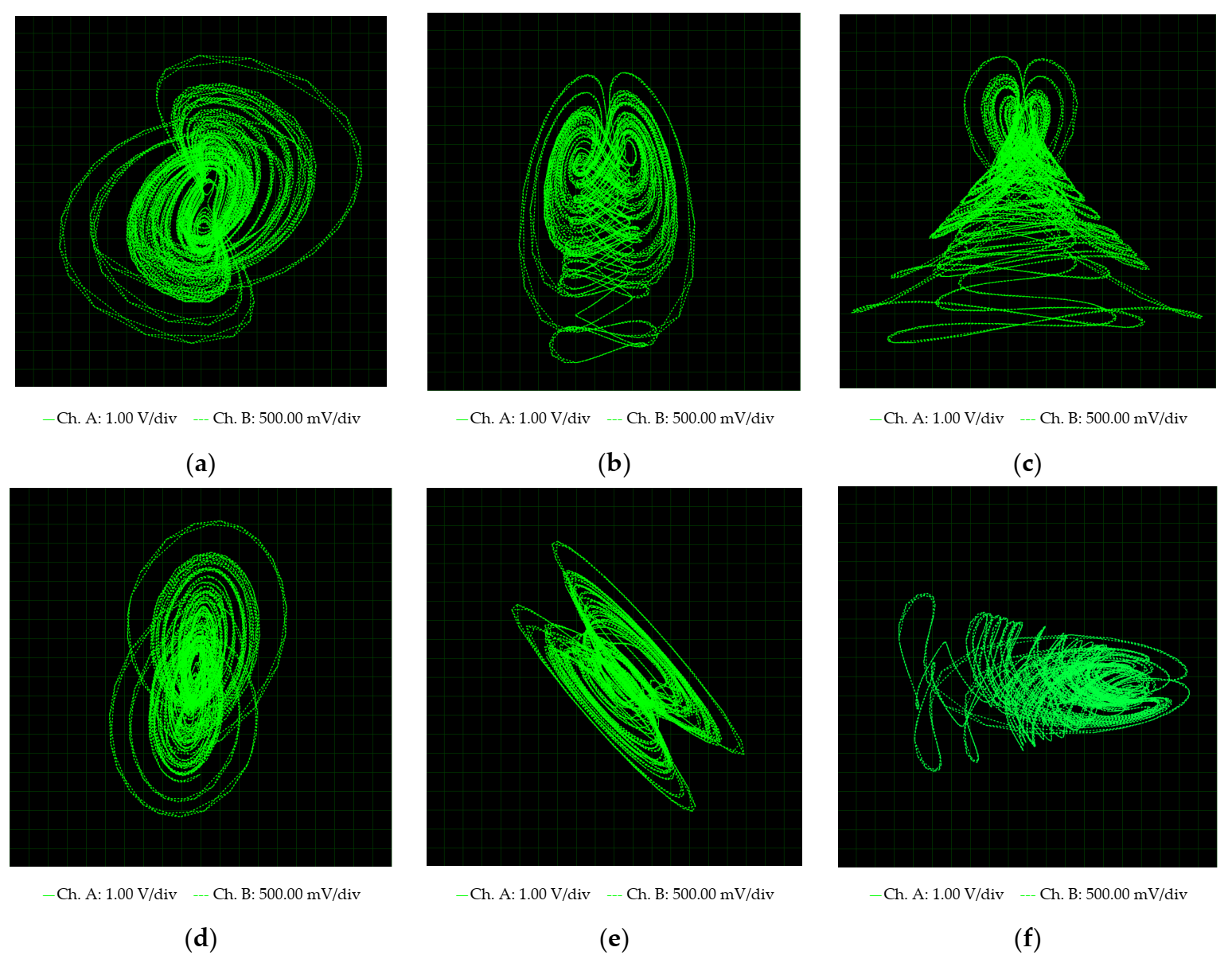
Electronics Free Full Text A New 4d Hyperchaotic System And Its Analog And Digital Implementation Html

9 If F X Y Z X Sin Yz A 2 Points Find The Gradient Off Homeworklib

1

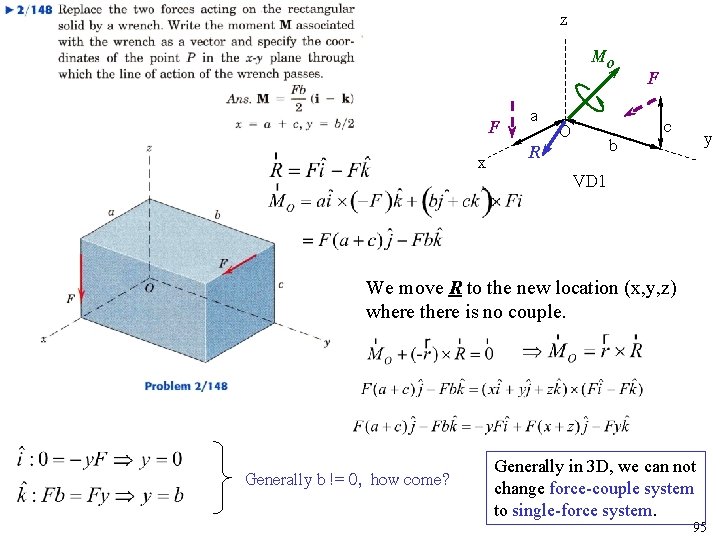
Force Systems 2 D Force Systems 3 D

Alphabet A B C D E F G H I J K L M N O

Magnetic Fields And Forces Facts About Magnetism N

Magnetic Fields And Forces Ppt Download

Academic Udayton Edu

Validation Of Identity Document Spain Questions Appsheet Creator Community

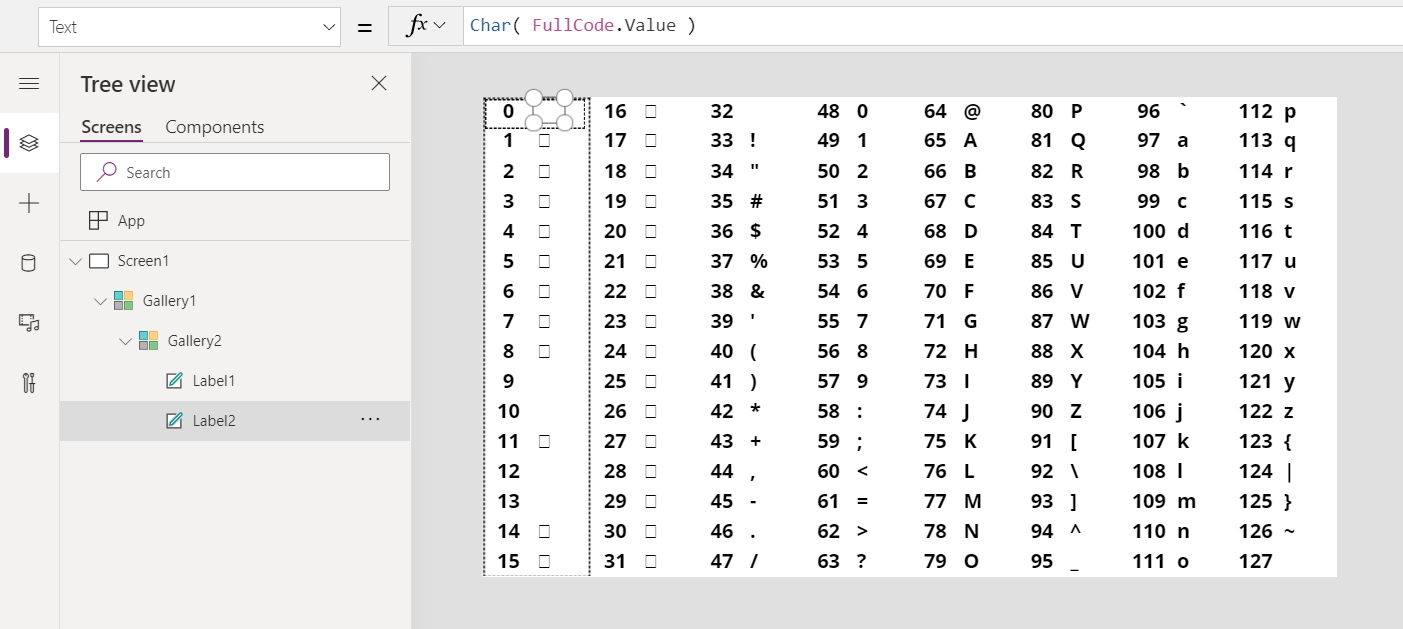
Char Function In Power Apps Power Apps Microsoft Docs

Math Wisc Edu

Logic Sheet 2 Grade B Lingustic Syntax En504 Studocu

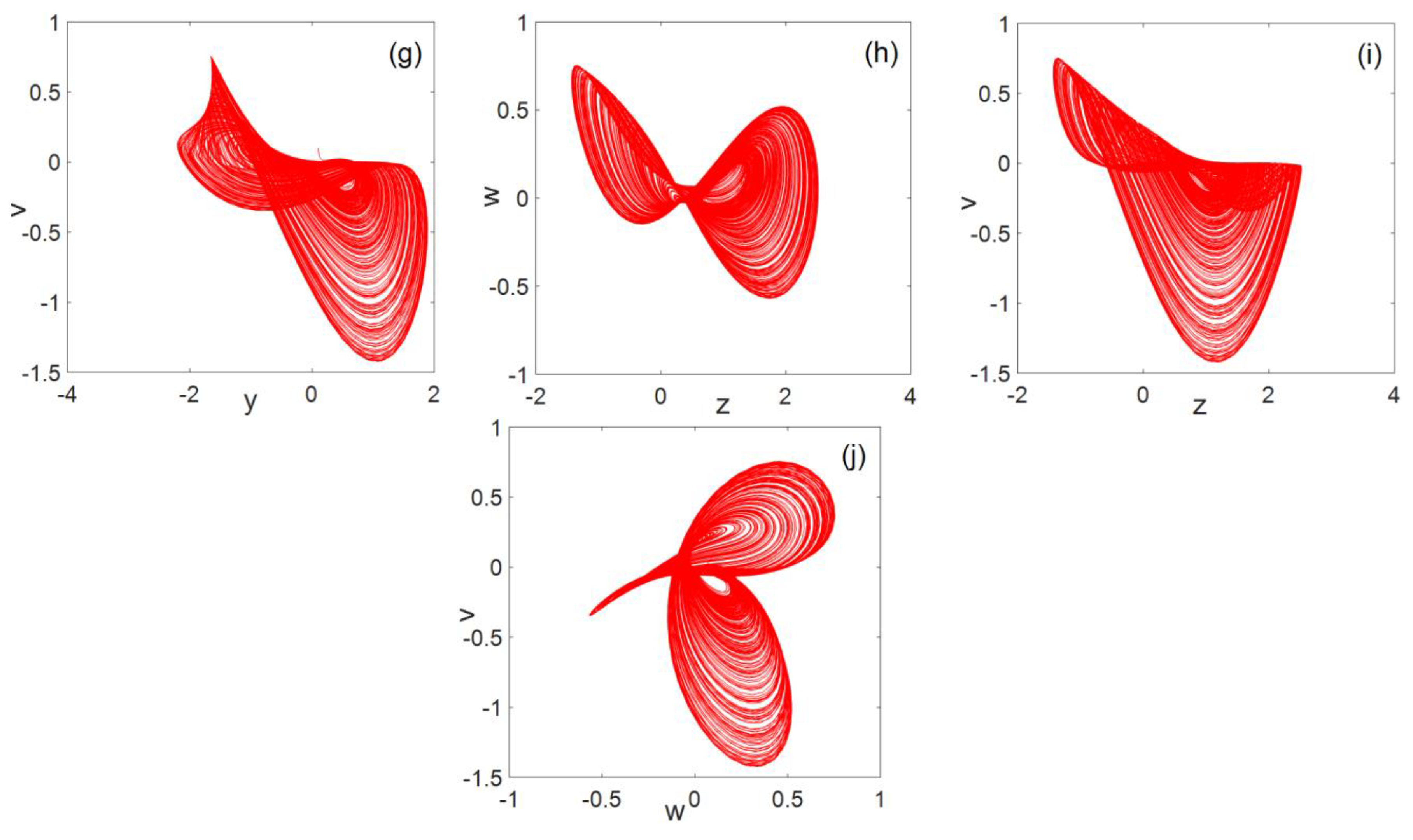
Entropy Free Full Text A Novel Five Dimensional Three Leaf Chaotic Attractor And Its Application In Image Encryption Html

Divergence Theorem

Math Jhu Edu

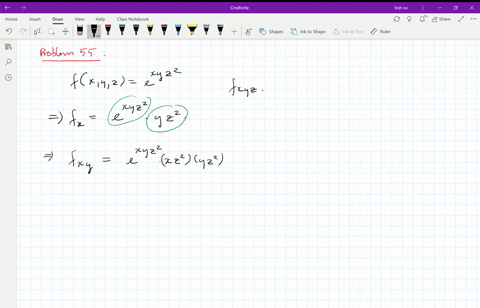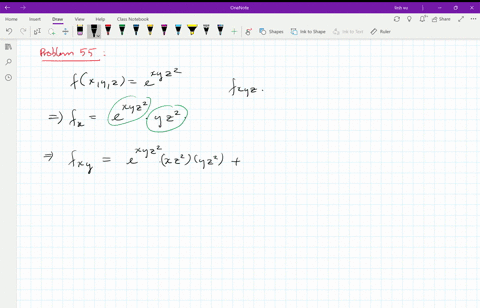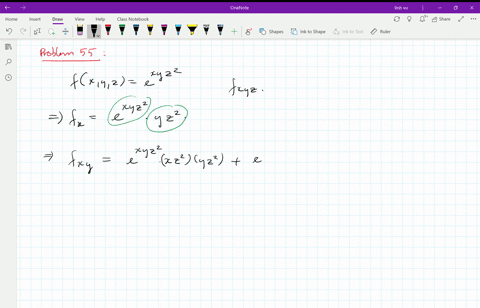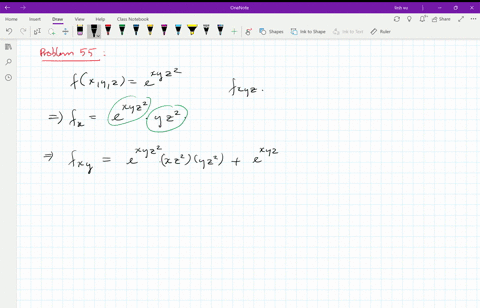
Solved Let Z F X Y X X U V Y Y U V And X 4 5 2 Y 4 5 3 Calculate The Partial Derivative In Terms Of A B C D E K P Q R S T W Begin Aligned F X 4 5 A

Differentiability For Functions Of Two Variables Local Linearity

Frequency Dependent Responses Of Neuronal Models To Oscillatory Inputs In Current Versus Voltage Clamp Biorxiv

Pdf Ohsx Xm511 Linear Algebra Multiple Choice Exercises For Chapter 2 Amol Patil Academia Edu

Registration 21 22 El Modena High School

Math Mcgill Ca

Math Mit Edu

Mathweb Math Ncu Edu Tw

Useful Resources Bizagi Glossary

Amazon Com Initials Wedding Cake Topper Letter Cake Topper Wedding Cake Topper A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Grocery Gourmet Food

Math Auckland Ac Nz

Solved Find Dz Dx And Dz Dy A Z F X G Y Dz Dx 0 0 F X Chegg Com

Math Mit Edu

5 Verify Stokes 39 Theorem For F X Y Z 2zi 3xj 5yk Over The Parabaloid B End仄curl Erds 6 Verify The Divergence Theorem For F X Y Z Zk Over The Hemisphere V 5 Verify Stokes 39

Tutorial 07 Analytic Functions Ma121 Cade Tut 7 Analytic Functions K R Kiran Hiremath Studocu

7 Show That The Following Functions U X Y Monic Functions V X Y And Determine F Z U X Y Iv X Y Are Harmoni Homeworklib

Dialectica Interpretation Wikipedia

Introduction To Artificial Intelligence Unit 5 Inference In

Validation Of Identity Document Spain Questions Appsheet Creator Community

Calc 501 1000 By James Bardo Issuu

About Us Pce Instruments

Search For Single Production Of A Vector Like T Quark Decaying To A Z Boson And A Top Quark In Proton Proton Collisions At Sqrt S 13 Tev Cern Document Server

Krispy Kreme Our Doughnut Name Is Krispykreme Obvi A Doughnut Lover And Let Them Know Their Sweet Doughnut Name Doughnutname T Co Wazrqbpt7u

Ucl Ac Uk

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Cartoon Text Font Hand Drawing Vector Letters Stock Illustration Download Image Now Istock